Олимпиадная задача Соловьёва: перемещения фигур и суммы на клетчатой бумаге (Планиметрия, 9-11 классы)

Выберем произвольную клетку и обозначим ее центр через O . Введем декартову систему координат с началом O , осями, параллельными линиям сетки и единичным отрезком, равным стороне клетки. Зафиксируем какие-либо положения данных фигур I и II и обозначим центры накрываемых ими клеток через A₁ , A₂ , A_m и B₁ , B₂ , B_n соответственно. Обозначим

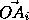= a_i, i=1,2, .., m, и = b_j, j=1,2, .., n.

Пусть c – произвольный вектор с целочисленными координатами, X – произвольная точка с целочисленными координатами, а g(X, c)– число, записанное в клетке с центром в конце вектора, отложенного от точки X и равного вектору c . Заметим, что

g(A_i, b_j)=g(B_j, a_i)=g(O, a_i+ b_j), (1)

где i=1,2, .., m , j=1,2, ..,n .

Пусть SI(X)( SII(X)) – сумма чисел, накрываемых первой (второй) фигурой, перенесенной из первоначального положения на вектор 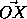. Тогда SI(X)= 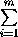g(X, a_i)и SII(X)= 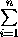g(X, b_j).

Рассмотрим сумму 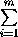SII(A_i)= 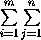g(A_i, b_j). Изменяя порядок суммирования и используя (1), получаем

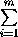SII(A_i)= 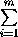g(B_j, a_i)= SI(B_j).

По условию задачи все слагаемые в сумме SI(B_j)положительны, так как каждое из них есть сумма чисел, накрываемых первой фигурой в некотором положении, значит, по крайней мере одно слагаемое в сумме 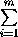SII(A_i)положительно, что и требовалось доказать.

Ответ задачи отсутствует