Олимпиадная задача по планиметрии 8-9 класс: вписанный четырехугольник Терешина

Задача

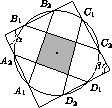
Внутри окружности расположен выпуклый четырехугольник, продолжения сторон которого пересекают ее в точках A₁ , A₂ , B₁ , B₂ , C₁ , C₂ , D₁ и D₂ 960. Докажите, что если A₁B₂=B₁C₂=C₁D₂=D₁A₂ , то четырехугольник, образованный прямыми A₁A₂ , B₁B₂ , C₁C₂ , D₁D₂ , можно вписать в окружность.

Решение

Пусть величины двух противоположных углов четырехугольников, образованного прямыми A₁A₂ , B₁B₂ , C₁C₂ и D₁D₂ , равны α и β . Нам достаточно показать, что α +β =π . Так как хорды A₁B₂ , B₁C₂ , C₁D₂ и D₁A₂ равны, то равны и угловые величины дуг A₁D₁B₂ , B₁A₁C₂ , C₁B₁D₂ , D₁C₁A₂ , которые мы обозначим через γ . Тогда по теореме о величине угла с вершиной вне круга

2α =A₁D₁B₂-A₂B₁=γ -A₂B₁, 2β =C₁B₁D₂-C₂D₁=γ -C₂D₁.

Сложив эти равенства, получим, что

2α +2β =2γ -(A₂B₁+C₂D₁)=2γ -(B₁A₁C₂+D₁C₁A₂-2π)=2π,

следовательно, α +β =π .

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии для 8-9 классов от Терешина Д. А.: Вписанный четырехугольник и окружность

Задача

Решение

Ответ

Подтверждение удаления