Математическая задача: можно ли получить x² + 10x + 9 из x² + 4x + 3? Олимпиадная задача 9-11 класс
Задача
Квадратный трёхчлен f(x) разрешается заменить на один из
трёхчленов 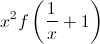 или
или 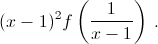 Можно ли с помощью таких операций из квадратного трёхчлена x² + 4x + 3 получить трёхчлен x² + 10x + 9?
Можно ли с помощью таких операций из квадратного трёхчлена x² + 4x + 3 получить трёхчлен x² + 10x + 9?
Решение
Решение 1:Пусть f(x) = ax² + bx + c. Заметим, что при допустимых операциях дискриминант трёхчлена не меняется: при первой операции f(x) меняется на трёхчлен (a + b + c)x² + (b + 2a)x + a с дискриминантом (b + 2a)² – 4a(a + b + с) = b² + 4ab + 4a2 – 4a² – 4ab – 4ac = b² – 4ac, а при второй – на трёхчлен
cx² + (b – 2c)x + (a – b + c) с дискриминантом (b – 2c)² – 4c(a – b + c) = b² – 4bc + 4c² – 4ac + 4bc – 4c² = b² – 4ac. Но у трёхчлена x² + 4x + 3 дискриминант равен 16 – 4·3 = 4, а у трёхчлена x² + 10x + 9 он равен 100 – 4·9 = 64; следовательно, получить из первого трёхчлена второй невозможно.
Решение 2:Положим 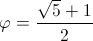 . Тогда φ = 1/φ + 1 = 1/φ–1, φ – 1 = 1/φ. Поэтому при выполнении разрешённых операций значение трёхчлена в точке φ умножается или делится на φ². Осталось заметить, что такими преобразованиями φ² + 4φ + 3 = 5φ + 4 не переводится в φ² + 10φ + 9 = 11φ + 10, поскольку отношение этих чисел меньше φ².
. Тогда φ = 1/φ + 1 = 1/φ–1, φ – 1 = 1/φ. Поэтому при выполнении разрешённых операций значение трёхчлена в точке φ умножается или делится на φ². Осталось заметить, что такими преобразованиями φ² + 4φ + 3 = 5φ + 4 не переводится в φ² + 10φ + 9 = 11φ + 10, поскольку отношение этих чисел меньше φ².
Решение 3:Нетрудно проверить, что данные преобразования взаимно обратны. Поэтому при положительном ответе на вопрос задачи один из данных трёхчленов можно было бы получить из другого применяя только первое преобразование (возможно, несколько раз). Но, как видно из решения 1, применяя первое преобразование к трёхчлену с натуральными коэффициентами мы будем получать снова трёхчлен с натуральными коэффициентами, а старший коэффициент будет возрастать. Поэтому снова получить приведённый трёхчлен не удастся.
Ответ
Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь