Олимпиадная задача по комбинаторной геометрии с принципом Дирихле для 8–10 классов
Задача
Квадратная доска разделена сеткой горизонтальных и вертикальных прямых на n² клеток со стороной 1. При каком наибольшем n можно отметить n клеток так, чтобы каждый прямоугольник площади не менее n со сторонами, идущими по линиям сетки, содержал хотя бы одну отмеченную клетку?
Решение
Оценка. Ясно, что если n клеток отмечены так, что выполняется условие задачи, то в каждой строке и в каждом столбце находится ровно одна отмеченная клетка. Считая, что n ≥ 3 (очевидно, что n = 2 – не наибольшее), возьмём строку A, в которой отмечена левая клетка, строку B, соседнюю с A,
и строку C, соседнюю либо с A (и не совпадающую с B), либо с B (и не совпадающую с A). Пусть b – номер отмеченной клетки в строке B. Ес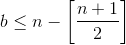ли 
или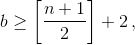 
то в строках A и B найдется прямоугольник площади, не меньшей n, не содержащий отмеченных клеток, следовательно, 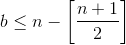. Рассмотрим два прямоугольника, образованных пересечением строк A, B и C со столбцами с номерами 
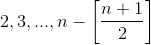и со столбцами с номерами 
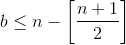В этих прямоугольниках не лежат отмеченные клетки строк A и B. Если n > 7, то площадь каждого из них не меньше n, но строка C содержит лишь одну отмеченную клетку, то есть один из этих прямоугольников не содержит отмеченных клеток. Итак, n ≤ 7.
Пример доски 7×7, удовлетворяющей условию задачи, приведён на рисунке.
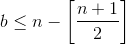
Ответ
При n = 7.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь