Олимпиадная задача по планиметрии и теории чисел: треугольник с простыми сторонами

  Пусть длины сторон треугольника равны a, b, c. Из формулы Герона имеем:  16S² = P(P – 2a)(P – 2b)(P – 2c),  где S – площадь, а  P = a + b + c  – периметр треугольника.

  Допустим, что S – целое число. Тогда P чётно (если P нечётно, то 16S² нечётно, что не так). Следовательно, либо числа a, b, c – чётные, либо среди них одно чётное и два нечётных.

  В первом случае, так как a, b, c – простые числа,  a = b = c = 2,  и площадь треугольника равна 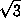  ,   то есть нецелая.

  Во втором случае будем считать, что  a = 2,  а b и c – нечётные простые числа. Если  b ≠ c,  то  |b – c| ≥ 2,  и неравенство треугольника не выполнено. Следовательно,  b = c.  Подставив, получим  S² = b² – 1,  или  (b – S)(b + S) = 1,  что невозможно для натуральных b и S.

Ответ задачи отсутствует