Олимпиадная задача по математике про турнир по теннису: условия для участников
Задача
В турнире по теннису n участников хотят провести парные (двое на двое) матчи так, чтобы каждый из участников имел своим противником каждого из остальных ровно в одном матче. При каких n возможен такой турнир?
Решение
Пусть описанный в задаче турнир проведён. Тогда все противники одного теннисиста разбиваются на пары, поэтому n нечётно. Все возможные пары противников разбиваются на четвёрки пар, игравших в одном матче. Следовательно, число ½ n(n – 1) этих пар кратно 4, откуда n – 1 = 8k.
Докажем, что при любом натуральном k указанный турнир для n = 8k + 1 участников возможен. При k = 1 для описания турнира поставим в соответствие теннисистам вершины правильного девятиугольника A1A2...A9. На рисунке изображён матч пары (A1, A2) против пары (A3, A5), причём отрезками соединены противники.
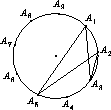
Ответ
n = 8k + 1, где k ∈ N.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь