Олимпиадная задача по функциям одной переменной для 10-11 класса (Токарев С. И.)

f(x)1, f(x) x . Заметив, что f(x)1удовлетворяет условию задачи, будем искать другие решения.

Пусть f(a)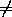1при некотором a>0. Тогда из равенств f(a)^f(xy)=f(a^xy)=f(a^x)^f(y)=f(a)^f(x)· f(y)следует, что

f(xy)=f(x)· f(y)(1)

для любых x , y>0. А тогда из равенств f(a)^f(x+y)=f(a^x+y)=f(a^x)· f(a^y)=f(a)^f(x)· f(a)^f(y)=f(a)^f(x)+f(y)следует, что

f(x+y)=f(x)+f(y)(2)

для любых x , y>0.

Из (1) имеем

f(1)=f(1· 1)=f(1)²,

т.е. f(1)=1, а затем из (2) и (1) получаем

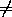f(n)=f(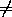1+..+1)=f(1)+..+f(1)=n, f()· n=f()· f(n)=f(m)=m,

т.е. для любых m , n

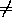
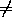
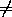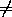f()=. (3)

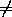Предположим, что для некоторого x>0имеет место неравенство f(x) x , скажем, f(x)<x (случай f(x)>x рассматривается аналогично). Подобрав число y= 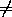так, чтобы выполнялись неравенства

f(x)<y<x,

из (2) и (3) получаем противоречащее им неравенство.

f(x)=f(y+(x-y))=f(y)+f(x-y)>f(y)=y.

Итак, сделанное выше предположение неверно, поэтому f(x)=x для любого x>0, и, разумеется, найденная функция годится.

1, x .