Олимпиадная задача по планиметрии о вписанной окружности и равенстве отрезков для 8-9 класса
Задача
В треугольник ABC с прямым углом C вписана окружность, касающаяся сторон AC, BC и AB в точках M, K и N соответственно. Через точку K провели прямую, перпендикулярную отрезку MN. Она пересекла катет AC в точке X. Докажите, что CK = AX.
Решение
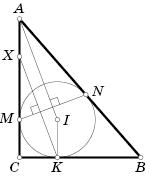
Пусть I – центр вписанной окружности треугольника ABC (см. рис.). Так как треугольник AMN равнобедренный, прямая IA является в нем не только биссектрисой, но и высотой, поэтому IA ⊥ MN, то есть IA || KX Заметим, что IK || AC. Значит, четырёхугольник AXKI – параллелограмм, то есть
AX = KI. Но KIMC – квадрат, откуда CK = KI = AX.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет