Олимпиадная задача по планиметрии для 9–11 класса от Заславского А. А.

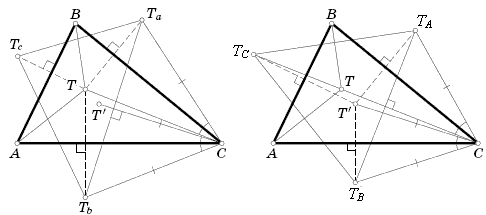
  Первый способ. Пусть T_a, T_b, T_c – точки, симметричные T относительно BC, CA, AB соответственно; T' – центр описанной окружности треугольника T_aT_bT_c. Так как  CT_a = CT = CT_b,  прямая CT' является серединным перпендикуляром к T_aT_b и биссектрисой угла T_aCT_b. Следовательно, прямые CT и CT' симметричны относительно биссектрисы угла C. Аналогично прямые BT и BT', AT и AT' симметричны относительно биссектрис соответствующих углов треугольника (рис. слева).

  Пусть теперь T_A, T_B, T_C – точки, симметричные T' относительно BC, CA, AB . Рассуждая, как выше, получаем, что T – центр описанной окружности треугольника T_AT_BT_C, а прямые AT, BT, CT являются серединными перпендикулярами к его сторонам. Значит, углы этого треугольника равны 60°, то есть этот треугольник правильный. Следовательно, точки T_A, T_B, T_C лежат соответственно на прямых AT, BT, CT, а симметричные им прямые проходят через T' (рис. справа).

 Второй способ. Заметим, что  ∠T_CAB= ∠TAC,  ∠T_CBA= ∠TBC,  то есть прямыеT_CAиCAсимметричны относительно биссектрисы углаTAB, а прямыеT_CBиCB– относительно биссектрисы углаTBA. Значит, точкиT_CиC изогонально сопряженыотносительно треугольникаTAB. ПосколькуCлежит на биссектрисе углаATBэтого треугольника,T_Cтоже лежит на этой биссектрисе, то есть прямаяCTпроходит черезT_C, а прямая, симметричная ей относительноAB, – черезT'. Аналогично черезT'проходят две другие прямые.

Ответ задачи отсутствует