Олимпиадная задача по теории алгоритмов и индукции для 9–11 классов от Петухова А. В.
Задача
С ненулевым числом разрешается проделывать следующие
операции: x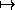
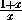 , x
, x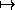
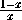 . Верно ли, что из каждого ненулевого
рационального числа можно получить каждое рациональное
число с помощью конечного числа таких операций?
. Верно ли, что из каждого ненулевого
рационального числа можно получить каждое рациональное
число с помощью конечного числа таких операций?
Решение
Обозначим наши операции через f(x)=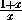 , g(x)=
, g(x)=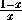 .
.
Докажем сначала, что, последовательно применяя их, мы можем получить операции, обратные к f и g .
Имеем f(g(f(x)))=-x и f(g(f(g(f(x)))))=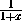 при x
при x
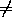 -1. Поэтому f(g(f(f(g(f(x))))))=x при x
-1. Поэтому f(g(f(f(g(f(x))))))=x при x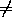 -1и f(g(f(g(f(g(x))))))=x при x
-1и f(g(f(g(f(g(x))))))=x при x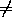 1.
1.
Далее, из 2 можно получить -2(и наоборот). Кроме того, f(-2)=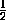 , g(
, g(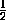 )=1. Значит, можно получить 1 из 2.
)=1. Значит, можно получить 1 из 2.
Так как g(-1)=-2, а из -2можно получить 2, можно получить 2 из -1.
Так как g(2)=-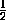 и f(-
и f(-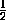 )=-1, можно получить -1из -2.
)=-1, можно получить -1из -2.
Итак, обратимость доказана.
Значит, достаточно доказать, что из единицы можно получить все
положительные рациональные числа. Докажем это индукцией по сумме
числителя и знаменателя несократимой дроби, представляющей наше
рациональное число 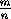 .
.
База индукции для m+n=2очевидна. Допустим, что при m+n<k число 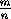 можно получить из единицы. Докажем, что тогда и
при m+n=k число
можно получить из единицы. Докажем, что тогда и
при m+n=k число 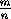 получается из единицы.
получается из единицы.
Если
m>n, то 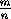 =1+
=1+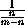 и n+(m-n)=m<m+n,
и n+(m-n)=m<m+n,
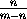 можно получить по предположению индукции.
Если же
можно получить по предположению индукции.
Если же
m<n, то 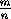 =
=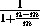 и(n-m)+m=n<m+n,
и(n-m)+m=n<m+n,
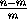 можно получить по предположению индукции.
Значит, в обоих случаях число
можно получить по предположению индукции.
Значит, в обоих случаях число 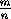 можно получить из
единицы, индукционный переход доказан.
можно получить из
единицы, индукционный переход доказан.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь