Олимпиадная задача по планиметрии для 8-9 класса: треугольники и периметры в квадрате
Задача
На сторонах единичного квадрата отметили точки K, L, M и N так, что прямая KM параллельна двум сторонам квадрата, а прямая LN – двум другим сторонам квадрата. Отрезок KL отсекает от квадрата треугольник периметра 1. Треугольник какой площади отсекает от квадрата отрезок MN?
Решение
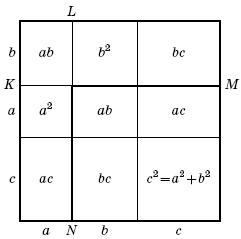
Решение 1:Пусть катеты первого треугольника равны a и b, а гипотенуза – c. Из рисунка видно, что удвоенная плошадь треугольника, отсекаемого отрезком MN, равна половине площади квадрата.

Решение 2:Пусть точки K, L, M, N лежат соответственно на сторонах AB, BC, CD, DA квадрата ABCD. Диаметр вневписанной окружности прямоугольного треугольника BKL, касающейся гипотенузы KL, равен его периметру (см. задачу 152553), поэтому эта окружность одновременно вписана в квадрат и её центр O – центр квадрата. Следовательно, высота треугольника OKL, опущенная на сторону KL, равна ½, а SOKL = c/2. Пусть P, Q, R, S – середины отрезков AB, BC, KM, LN, а T – точка пересечения отрезков KM и LN. Нам достаточно доказать, что SABCMTN = ½, т.е. что SBQRTSP = c/2 (поскольку SAPSN = a/2, SCQRM = b/2). Но это так и есть:
SBQRTSP = 2SKLT + 2SKTP + 2SLTQ = 2(SKLT + SKTO + SLTO) = 2SKLO = ½.
Ответ
¼.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь