Олимпиадная задача по планиметрии и комбинаторной геометрии: нестандартный шестиугольник на клетчатой бумаге
Задача
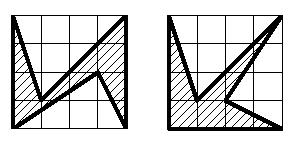
На клетчатой бумаге отмечены четыре узла сетки, образующие квадрат 4*4. Отметьте ещё два узла и соедините их замкнутой ломаной так, чтобы получился шестиугольник (не обязательно выпуклый) площади 6 клеток.
Решение
Можно попытаться найти решение, просто пробуя различные пары вершин внутри квадрата 4*4 и стараясь сделать получаемый шестиугольник поуже. При этом удобнее считать не площадь шестиугольника, а площадь оставшейся части квадрата - она должна быть равна 10 клеткам.
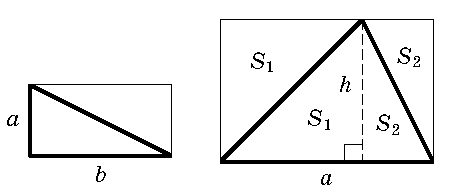
Для подсчёта площади можно разбить оставшуюся часть на прямоугольные треугольники и вспомнить, что площадь прямоугольного треугольника, катеты которого идут по линиям сетки, равна половине площади прямоугольника со сторонамиaиb(см. рис. слева) и равнаab/2 (эта формула верна и для произвольного прямоугольного треугольника). Те из вас, кто знает более общую формулу: площадь треугольника со сторонойaи опущенной на неё высотойhравнаah/2 (см. рис. справа), могут сразу найти площадь произвольного треугольника, не разбивая его на прямоугольные.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь