Может ли квадрат быть развёрткой треугольной пирамиды? Олимпиадная задача 10–11 класс

  Рассмотрим квадрат AD₁D₂D₃, в котором точки В и С – середины сторон D₁D₂ и D₂D₃ соответственно (см. рис.). При его сгибании по прямым АВ, ВС и АС точки D₁, D₂ и D₃ совместятся в одной точке D, образуя пирамиду ABCD.

  Осталось показать, что пирамида будет "невырожденной", то есть точкиА, В, СиDне окажутся в одной плоскости. Ввиду симметрии достаточно проверить, что  ∠ВАD₂< ∠ВАD₁.   Первый способ. В треугольнике AD₁D₂  АВ – медиана, AD₁ – высота, биссектриса, проведённая из вершины А, лежит между ними, поэтому

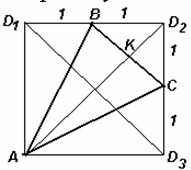
∠ВАD₁ > ∠ВАD₂.   Второй способ. Пусть O – центр квадрата. Поскольку, очевидно,  AO > BO,  то  ∠ВАD₁ = ∠АBO > ∠BAO = ∠ВАD₂.

Ответ задачи отсутствует