Олимпиадная задача по планиметрии и теории чисел: периметры квадрата и прямоугольника

  Пусть a – сторона квадрата, а стороны прямоугольника – k и l. Отношение их периметров  ^2(k+l)/_4a.  При этом  a² = kl,  ^2(k+l)/_4a = ^a²+k²/_2ak = ½ (^a/_k + ^k/_a).

  Пусть это число – целое. При этом  ^a/_k = x  – рациональное число. Тогда  x + ¹/_x – чётное число 2n.  x + ¹/_x = 2n,  x² – 2nx + 1 = 0,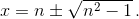 

  Если x рационально, то число 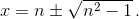   – целое. Итак, x и ¹ /_x = 2n – x  – целые. Но единственное целое, обратное целому, равно 1.

Ответ задачи отсутствует