Решение олимпиадной задачи по алгебре для 9–11 классов: сложное уравнение
Задача
Решить уравнение (x² – x + 1)4 – 10x²(x² – x + 1)² + 9x4 = 0.
Решение
Пусть y= (x² –x+ 1)², тогда y² – 10x²y+ 9x4= 0. Решив это уравнение относительноy, получим: y1= 9x², y2=x². Итак, данное уравнение свелось к двум следующим: (x² –x+ 1)² = 9x² и (x² –x+ 1)² =x², то есть к четырём квадратным уравнениям: x² –x+ 1 = 3x, x² –x+ 1 = – 3x, x² –x+ 1 =x, x² –x+ 1 = –x.
Ответ
–1, 1, 2 – 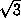 , 2 +
, 2 + 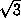 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет