Олимпиадная задача по стереометрии: минимальная поверхность вращения треугольника ABC

Для начала найдём площадь поверхности полученного тела вращения. Площадь боковой поверхности конуса, образованного вращением CD , равна π· CD² sinα . Тогда площадь поверхности, образованной вращением отрезка AC вокруг оси y будет составлять π CD² sinα-π (CD-3)² sinα=π sinα· (6CD-9)=π sinα((6· 10)/ sinα-9)=π(60-9 sinα).

Угол между y и направлением катета BC равен90^o+α . Теперь аналогично мы можем вычислить площадь поверхности, образованной вращением BC . Она равна π sin(α+90^o)((8· 10)/( sin(α+90^o))-16)=π(80-16 cosα).

Осталось вычислить площадь поверхности, образуемой вращением отрезка AB . Угол между прямой y и направлением отрезка AB равен α-β , где β=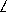 BAC . Тогда sin(α-β)= sinα cosβ- sinβ cosα=3/5 sinα-4/5 cosα . Расстояние AA_y равно10-AC sinα=10-3 sinα . Теперь мы можем вычислить искомую площадь. Она равна π(10·(10-3 sinα)+25·(3/5 sinα-4/5 cosα))= π(100-15 sinα-20 cosα).

Таким образом, площадь поверхности всей фигуры вращения треугольника ABC вокруг оси y равна π(60-9 sinα+80-16 cosα+100-15 sinα-20 cosα)=π(240-12(2 sinα+3 cosα)).

Отметим, что если бы точка A или B лежала по другую сторону от прямой, проходящей через вершину C параллельно прямой y , то формула для площади получилась бы другой. Получились бы другие знаки слагаемых в формуле для площади поверхности тела вращения. Однако все они сводятся к выведенной формуле, если позволить углу α изменяться от0^o до360^o .

Итак, минимум площади будет достигаться при максимуме выражения2 sinα+3 cosα=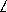 sin(α+ϕ), где вспомогательный угол ϕ= arctg3/2 . Это выражение достигает максимума при α+ϕ=π/2. Откуда α=π/2- arctg3/2= arctg2/3 .

α= arctg2/3 .