Делимость многочленов: олимпиадная задача по математике для 10–11 классов

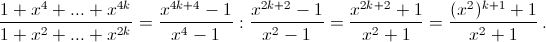  Если  k + 1  нечётно, числитель делится на знаменатель, а если

k + 1 = 2n,  при делении получается остаток 2, поскольку  x²(k+1) – 1 = x⁴ⁿ – 1  делится на  x⁴ – 1,  а значит, и на  x² + 1.

При чётном k делится, а при нечётном – нет.