Назад

Олимпиадная задача по стереометрии: поверхность пирамиды с равными периметрами граней

Задача 209156 • Сложность: 3 • 10-11 класс
Задача

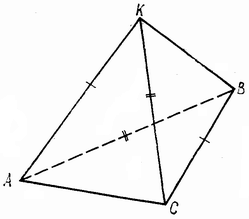
В треугольной пирамиде периметры всех её граней равны. Найти площадь полной поверхности этой пирамиды, если площадь одной её грани равна S .

Разделы:
Стереометрия
Источники:
Белорусские республиканские математические олимпиады Олимпиады и турниры
Количество версий:
5
Решение

Допустим, что известна площадь грани ABC=S (рис.). Запишем, что периметры всех граней равны:

AK+KB+AB=AB+AC+CB, (1)

AK+KC+AC=KC+CB+KB, (2)

AK+KB+AB=KB+BC+KC. (3)

Сложив равенства (1) и (2) почленно, найдем, что AK=BC . Подставив вместо AK в равенство (3) BC , найдем, что AB=KC . Затем из (1) AC=KB . Отсюда легко получается, что все грани тетраэдра равны между собой, а площадь его поверхности равна4S .

Ответ

4S .

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет