Олимпиадная задача по стереометрии для 10-11 класса: сечение тетраэдра
Задача
Ребро правильного тетраэдра равно a . Найти стороны и площадь
сечения, параллельного двум его скрещивающимся рёбрам и отстоящего
от центра тетраэдра на расстояние b , причём0<b<a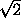 /4.
/4.
Решение
Секущая плоскость PEFK параллельна прямой SC , а потому
пересекается с гранями, в которых лежит ребро SC , по прямым,
параллельным ребру SC : EF||SC, PK||SC (рис.). По аналогичной
причине секущая плоскость пересекается с гранями, содержащими ребро AB , по прямым, параллельным этому ребру: PE||AB, KF||AB . Таким
образом, в сечении получается параллелограмм. Поскольку же
непересекающиеся ребра в правильном тетраэдре взаимно
перпендикулярны ( AB SC ), то в сечении получается прямоугольник PEFK . Проведем SM
SC ), то в сечении получается прямоугольник PEFK . Проведем SM пл. ABC . Плоскость SCM перпендикулярна
к плоскости основания; AB
пл. ABC . Плоскость SCM перпендикулярна
к плоскости основания; AB пл. SCD . Поэтому KF
пл. SCD . Поэтому KF пл. SCD , так как KF||AB .
пл. SCD , так как KF||AB .
Далее пл. SCD пл. PEFK , в которой лежит прямая,
перпендикулярная к первой плоскости. Эти плоскости пересекаются по
прямой NT||SC ; проведём DJ
пл. PEFK , в которой лежит прямая,
перпендикулярная к первой плоскости. Эти плоскости пересекаются по
прямой NT||SC ; проведём DJ SC , DJ
SC , DJ пл. PEFK , так как DJ
пл. PEFK , так как DJ KF и DJ
KF и DJ NT, KF||AB, NT||SC . O – центр тетраэдра,
так как это точка пересечения высоты тетраэдра SM со срединным
перпендикуляром ребра SC (или с биссектрисой угла SDC ). OL=b ,
где L – точка пересечения DJ с плоскостью сечения. DC=SD=a
NT, KF||AB, NT||SC . O – центр тетраэдра,
так как это точка пересечения высоты тетраэдра SM со срединным
перпендикуляром ребра SC (или с биссектрисой угла SDC ). OL=b ,
где L – точка пересечения DJ с плоскостью сечения. DC=SD=a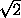 /2, MC=a
/2, MC=a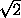 /3,
SM=a
/3,
SM=a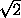 /3(из треугольника MCS ). Из равнобедренного
треугольника SDC находим DJ=a
/3(из треугольника MCS ). Из равнобедренного
треугольника SDC находим DJ=a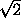 /2. Из подобия
треугольников MSC и JSO найдем OJ: SJ/OJ=MS/MC , откуда OJ=a
/2. Из подобия
треугольников MSC и JSO найдем OJ: SJ/OJ=MS/MC , откуда OJ=a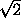 /4.
Отсюда LJ=OJ-OL=a
/4.
Отсюда LJ=OJ-OL=a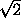 /4-b , DL=DJ-LJ=a
/4-b , DL=DJ-LJ=a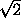 /2-(a
/2-(a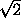 /4-b)=(a
/4-b)=(a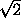 +4b)/4.
+4b)/4.
Теперь можем определить высоту прямоугольника NT из подобия
треугольников SCD и NTD : NT/SC=DL/DJ,
NT=(a+2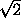 b)/2. Основание прямоугольника PEFK определим из подобия треугольников ABC и KFC , для чего сначала
найдем TC=DC-DT . DT определяется из прямоугольного треугольника DLT :
b)/2. Основание прямоугольника PEFK определим из подобия треугольников ABC и KFC , для чего сначала
найдем TC=DC-DT . DT определяется из прямоугольного треугольника DLT :
DT=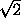 ,; LT=NT/2,;
DT=(
,; LT=NT/2,;
DT=(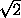 (a+2
(a+2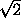 b))/4,
b))/4,
TC=(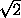 (a-2
(a-2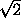 b))/4, KF=(a-2
b))/4, KF=(a-2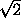 b)/2.
b)/2.
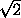
Ответ
сечение – прямоугольник со сторонами (a+2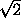 b)/2, (a-2
b)/2, (a-2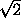 b)/2и площадью (a2-8b2)/4.
b)/2и площадью (a2-8b2)/4.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь