Олимпиадная задача по математике: Решить уравнение x² + 3x + 9 = 9n² в целых числах

  Решим уравнение относительно x: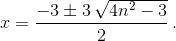  

  Необходимо, чтобы подкоренное выражение было полным квадратом:  4n² – 3 = k²,  4n² – k² = 3,  (2n – k)(2n + k) = 3.  Достаточно рассмотреть случай, когда n и k неотрицательны. Тогда  2n – k = 1,  2n + k = 3,  4n = 4.

  Итак,  n = ± 1,  x = 0  или   x = –3.

(0, ±1),  (–3, ±1).