Олимпиадная задача по стереометрии: высоты треугольной пирамиды для 10-11 классов

Пусть SO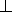 пл. ABC , CP 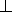пл. SAB , K – точка пересечения этих перпендикуляров. Обе высоты лежат в плоскости CSK , которая перпендикулярна как к плоскости ASB , так и к плоскости ABC . Поэтому грани ASB и ABC пересекаются по ребру, перпендикулярному к плоскости SKC : AB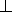 пл. SKC . Следовательно, AB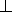 SC (рис.).

Можно показать обратное. Если два противоположных ребра тетраэдра взаимно перпендикулярны, то высоты тетраэдра, опущенные из концов одного из них, должны пересечься. Поскольку ребра тетраэдра здесь равноправны, то из этого следует, что и две другие высоты тетраэдра пересекутся. Пусть AB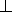 SC . Проведем SN 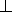AB , пл. CSN 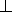AB , следовательно, пл. ASB 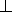пл. NSC . Поэтому перпендикуляр к плоскости ASB лежит в плоскости NSC . 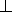Плоскость NSC перпендикулярна и к плоскости ABC , в которой также лежит AB пл. NSC . Поэтому и перпендикуляр к плоскости ABC лежит в плоскости NSC . Поскольку две высоты лежат в одной плоскости, то они пересекутся.

Вместо доказательства обратного предложения можно было непосредственно его вывести из перпендикулярности ребер AB и SC и того, что высоты, опущенные из точек A и B , пересекутся. Для этого в предыдущем рассуждении необходимо изменить роли рёбер AB и SC .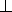

Ответ задачи отсутствует