Олимпиадная задача по стереометрии для 8-9 класса — расстояние отрезка до плоскости

Пусть A1, B1и M1– ортогональные проекции на плоскость α точек A и B и середины M отрезка AB соответственно. Тогда расстояние от точки M до плоскости α равно длине отрезка MM1.

Если точки A и B расположены по одну сторону от плоскости α , то MM1– средняя линия прямоугольной трапеции AA1B1B с основаниями AA1и BB1. Следовательно,

MM1 = 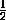(AA1 + BB1) = 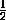(1 + 3) = 2.

Если точки A и B расположены по разные стороны от плоскости α , то MM1– отрезок, соединяющий середины диагоналей прямоугольной трапеции AA1BB1с основаниями AA1и BB1. Следовательно,

MM1 = 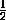|AA1 - BB1| = 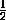(3 - 1) = 1.

2 или 1.