Решение системы алгебраических уравнений из 50 переменных — олимпиадная задача
Задача
Решить систему уравнений 1 − x1x2x3 = 0,
1 + x2x3x4 = 0,
1 − x3x4x5 = 0,
1 + x4x5x6 = 0,
...
1 − x47x48x49 = 0,
1 + x48x49x50 = 0,
1 − x49x50x1 = 0,
1 + x50x1x2 = 0.
Решение
Ясно, что ни одно из неизвестных не равно нулю. Вычитая из первого уравнения второе, получим x2x3(x1 + x4) = 0, то есть x1 = – x4. Аналогично
x2 = – x5, x3 = – x6, ..., x47 = – x50, x48 = – x1, x49 = – x2, x50 = – x3. Отсюда видно, что x1 = x7, x2 = x8, ..., x50 = x6. Продолжая, получим
x1 = x3 = x5 = ... = x49 = – x2 = – x4 = ... = – x50. Подставив эти формулы, например, в первое уравнение, получим 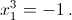
Ответ
(–1, 1, –1, 1, ..., –1, 1).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет