Олимпиадная задача по планиметрии: минимум суммы радиусов вокруг треугольников ABM и CBM

1-й способ. Пусть M – некоторая точка на прямой AC , O₁ – центр окружности, описанной вокруг треугольника ABM , радиус которой R₁ ; O₂ – центр окружности, описанной вокруг треугольника BMC радиуса R₂ , H – основание высоты треугольника ABC (рис. 1). Воспользуемся формулой для радиуса описанного круга: R=abc/4S , где a,b,c – стороны треугольника, S – его площадь. Применим эту формулу к треугольникам ABM и MBC , введя предварительно обозначения: AB=c, BC=a, AM=k, MC=e, BM=p, BH=h . Тогда R₁=cpk/4S _AMB, R₂=pae/4S _BMC, S _AMB=1/2 kh, S _MBC=1/2 eh . Подставив в формулы для радиусов описанных окружностей значения площадей соответствующих треугольников, получим для суммы этих радиусов выражение R₁+R₂=cpk/2kh+pae/2eh=p/2h(c+a) . В этом выражении переменной является лишь длина расстояния от точки B до точки M , т. е. p . Поэтому сумма радиусов принимает наименьшее значение при минимуме этого расстояния, когда точка M совпадет с основанием высоты треугольника ABC , т. е. с точкой H .

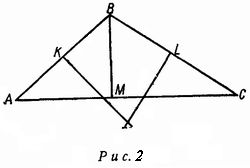
2-й способ. Центр окружности, описанной вокруг угольника ABM , лежит на перпендикуляре к стороне, проведенном через середину этой стороны K (рис. 2). Отсюда ясно, что минимальным радиусом такой окружности будет половина стороны AB . При этом треугольник ABM прямоугольный. Но в этом случае и треугольник BMC будет прямоугольным и радиус окружности, описанной вокруг него, также будет минимальным. Отсюда ясно, что если в качестве точки M взять на стороне AC основание высоты треугольника ABC , то сумма радиусов окружностей, описанных вокруг треугольников ABM и BMC , будет наименьшей.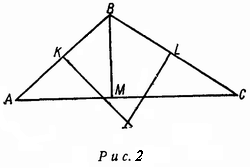

Ответ задачи отсутствует