Олимпиадная задача по комбинаторной геометрии: размещение точек в треугольнике
Задача
k точек на плоскости расположены так, что любой треугольник с вершинами в этих точках имеет площадь не больше 1. Доказать, что все эти точки можно поместить в треугольник площади 4.
Решение
Из данных k точек выбираем 3 такие, что треугольник с вершинами в
данных точках имеет наибольшую площадь из всех треугольников с
вершинами в данных k точках. Пусть это будут точки A,B,C (рис.).
Проведём через точку B прямую LN||AC . Каждая из k точек будет
лежать по ту же сторону от прямой LN , что и треугольник ABC , ибо
иначе площадь треугольника с вершиной в этой точке и основанием AC была бы больше площади треугольника ABC . Проведя через точку A прямую LM||BC и через точку C прямую MN||AB , точно так же
докажем, что все k точек лежат по ту же сторону от прямых LM и MN , что и точки A,B,C . Следовательно, все k точек будут лежать
внутри треугольника LMN . Площадь этого треугольника состоит из
площадей четырёх равных треугольников. Поскольку площадь одного из
них не превосходит единицы, то площадь всего треугольника LNM не
превосходит четырёх.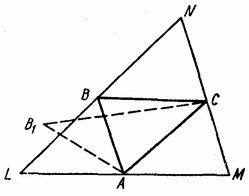
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь