Олимпиадная задача по планиметрии на площадь четырёхугольника для 8–9 классов

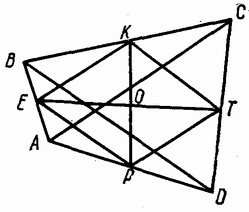
Соединим последовательно середины сторон данного четырёхугольника E , K,T,P (рис.). Полученный четырёхугольник EKTP есть ромб, ибо его стороны равны половинам диагоналей как средние линии треугольников ABC,ADC,BCD , ABD , а диагонали данного четырёхугольника по условию равны a . Далее средние линии указанных треугольников отсекают от них треугольники с площадью, в 4 раза меньшей, чем площади этих треугольников, т.е. S _BEK=1/4S _BAC, S _PTD=1/4S _ACD, S _KCT=1/4S _DBC, S _AEP=1/4S _ABD . Сложив площади первых двух треугольников, а затем вторых, получим:

S _BEK+S _PTD=1/4(S _ABC+S _ACD)=1/4S_ABCD,

S _KCT+S _AEP=1/4(S _DBC+S _ABD)=1/4S_ABCD.

Сумма площадей всех четырёх треугольников, дополняющих ромб, равна половине площади четырёхугольника. Следовательно, площадь данного четырёхугольника равна удвоенной площади ромба. Площадь ромба равна полупроизведению его диагоналей, а площадь данного четырёхугольника – произведению диагоналей ромба, каковыми являются средние линии данного четырёхугольника. Если обозначим средние линии через x и y , то из треугольника, например, OEK найдём, что x²+y²=a², (x+y)²=a²+2xy, xy=((x+y)²-a²)/2=(b²-a²)/2 .

(b²-a²)/2 .