Олимпиадная задача по планиметрии для 8-10 классов: трапеция и отношение площадей
Задача
Трапеция, основания которой равны a и b (a > b), рассечена прямой, параллельной основаниям, на две трапеции, площади которых относятся как k : p. Найти длину общей стороны образовавшихся трапеций.
Решение
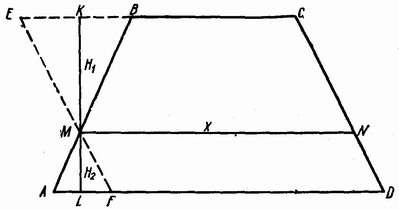
Обозначим длину отрезка MN через x (см. рис.). Проведём через точку M прямые EF || CD и KL ⊥ AD . Длину отрезка KM обозначим через H1, длину отрезка ML – через H2. Тогда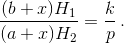 
Из подобия треугольников EMB и FMA MK : ML = EB : AF, или H1/H2 = x–b/a–x. Следовательно,
x–b/a–x = k(a+x)/p(b+x), откуда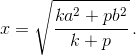 
Ответ
.
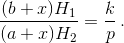Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет