Олимпиадная задача по планиметрии: точки на плоскости и соотношения расстояний

Решим задачу координатным методом. Введём систему координат таким образом, чтобы A находилась в начале координат, а B имела координаты (1,0) . Пусть точка M(x,y) – искомая. Тогда 1/3=MB/MA=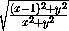 . Отсюда получаем x²+y²=9((x-1)²+y²) , 8x²-18x+8y²+9=0 ,

x²-9/4 x+y²+9/8=0; x²-2·9/8 x+(9/8)²+y²+9/8-(9/8)²=0;

(x-9/8)²+y²=(9/8)²-9/8.

Получили уравнение окружности. Следовательно, все точки M данного множества лежат на окружности. Далее, так как все наши преобразования были равносильными, то любая точка, лежащая на окружности, заданной получившимся уравнением, будет принадлежать данному множеству.

Ответ задачи отсутствует