Олимпиадная задача по планиметрии: пересечение прямых PK на дуге AB для 8–9 классов
Задача
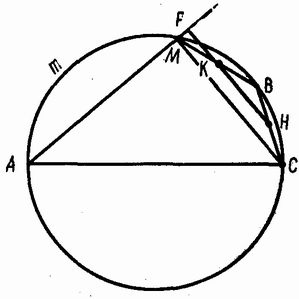
На дуге AB есть произвольная точка M. Из середины K отрезка MB опущен перпендикуляр KP на прямую MA.
Доказать, что все прямые PK проходят через одну точку.
Решение
Проведём диаметр AC и точку B соединим с точкой C (см. рис.). Продолжим прямую PK до пересечения с прямой BC в точке H. ∠AMC = 90°, значит,
PH || MC. Отрезок KH проходит через середину стороны MB треугольника MBC параллельно стороне MC, поэтому он является средней линией треугольника BMC, то есть BH = HC. Итак, все прямые PK проходят через середину фиксированного отрезка BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет