Олимпиадная задача по планиметрии и принципу крайнего для классов 8–11: Доказательство расположения точек на одной прямой
Задача
На плоскости дано k точек, расположенных так, что на каждой прямой, соединяющей две из этих точек, лежит по крайней мере ещё одна из них. Доказать, что все k точек лежат на одной прямой.
Решение
Предположим противное: не все k отмеченных точек лежат на одной прямой. Рассмотрим множество всех прямых, проходящих через как минимум 2 отмеченные точки. Рассмотрим все возможные расстояния от наших точек до этих прямых. По предположению, не все они равны нулю. Среди положительных расстояний выберем наименьшее. Пусть это расстояние будет между точкой D и прямой l , содержащей точки A,B и C (рис.). В полученном треугольнике ADC опустим высоту DH на прямую l . По одну сторону от H на прямой должно находиться как минимум две отмеченные точки (будем считать, что сама H расположена сразу с обеих сторон). Без ограничения общности положим, что это точки A и B (как на рисунке).
Покажем, что расстояние от B до прямой AD будет строго меньше,
чем DH . Действительно, расстояние от H до прямой AD строго
меньше DH , поскольку высота всегда меньше двух прилегающих к ней
сторон. А расстояние от B до AD , очевидно, не больше расстояния
от H до AD . Тем самым мы показали, что выбранное нами расстояние
вовсе не минимально. Получили противоречие. Следовательно, все
отмеченные точки лежат на одной прямой.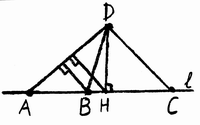
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь