Олимпиадная задача по планиметрии: неравенство для сторон треугольника (8–10 класс)
Задача
Стороны треугольника a,b и c . 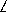 A=60o . Доказать, что
A=60o . Доказать, что
3/(a+b+c)=1/(a+b)+1/(a+c).
Решение
Преобразуем данное выражение:
3/(a+b+c)=1/(a+b)+1/(a+c),
3(a+b)(a+c)=(a+b+c)(2a+b+c),
3a2+3ac+3ab+3bc=(a+b+c)2+a(a+b+c),
a2+bc=b2+c2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет