Олимпиадная задача по планиметрии: построение треугольника с перпендикулярными медианами

Пусть искомый треугольник построен. AM=MC, BK=KC, AK MB . Из прямоугольных треугольников AMO и OKB запишем: OM²+OA²=AM², OK²+OB²=KB², AC=2b, AM=b, BC=2a , KB=a , AK=3x, AO=2x , MB=3y, OB=2y, OM=y, OK=x (рис.)

Подставим введённые значения в данные уравнения

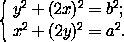
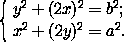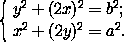Решая эту систему, получим x=/ , y=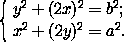/ 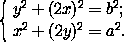. Достаточно построить один из этих отрезков, чтобы построить треугольник по двум сторонам и медиане. Отрезк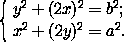и и 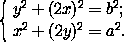a можно построить с помощью теоремы Пифагора. Теперь же x=(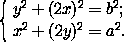· a)/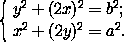a , очевидно, можно построить.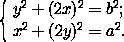

Ответ задачи отсутствует