Олимпиадная задача по планиметрии для 8–9 классов: площадь шестиугольника
Задача
На катетах и гипотенузе прямоугольного треугольника построены квадраты, расположенные вне треугольника. Вычислить площадь шестиугольника, вершины которого совпадают с теми вершинами квадратов, которые не принадлежат данному треугольнику. Длина гипотенузы c и сумма длин катетов s известны.
Решение
Продолжим сторону EA и опустим на неё перпендикуляр FP . Продолжим также сторону CL и опустим на неё перпендикуляр KT (рис.).
Треугольники TCK и PFA равны треугольнику ABC (по гипотенузе и
острому углу, например,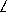 
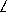FAP= BAC как углы со взаимно
перпендикулярными сторонами). Треугольник BMN равен треугольнику ABC . Треугольник EAF равновелик треугольнику AFP , треугольник LCK равновелик треугольнику CTK , так как FA есть медиана
треугольника EFP , а CK – медиана треугольника TKL . Поэтому
площадь нашего шестиугольника состоит из площади трёх квадратов и
четырёх равновеликих треугольников. Если длину катетов обозначить
соответственно через a и b , то площадь шестиугольника будет
равна
a2+b2+c2+4ab/2=a2+b2+2ab+c2=(a+b)2+c2=s2+c2.
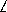
Ответ
s2+c2 .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь