Олимпиадная задача по стереометрии для 10-11 класса: минимальный отрезок EF на кубе
Задача
На диагонали AC нижней грани единичного куба ABCDA1B1C1D1 отложен отрезок AE длины l . На диагонали B1D1 его верхней грани отложен отрезок B1F длиной ml . При каком l (и фиксированном m>0 ) длина отрезка EF будет наименьшей?
Решение
Отрезок FE определим из треугольника FKE , где FK перпендикулярен плоскости ABCD , FK=1, FE=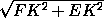
(рис.). Из треугольника KEO , где угол KOE равен 90o как угол
между диагоналями квадрата, находим EK2=KO2+OE2,
OK=FL=B1F-LB1=ml-
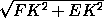/2 ; OE=AO-AE=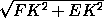/2-l . Отсюда EK2=(ml-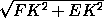/2)2+(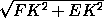/2-l)2=l2(m2+1)-l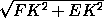(m+1)+1 .
Подставим значение EK2 и FK2 в формулу для FE :
FE=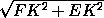
.
2+l2(m2+1)-l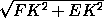(m+1)=
=(m2+1)(l2-2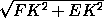/2·
(m+1)/(m2+1)l+((m+1)2)/(2(m2+1)2)-((m+1)2)/(2(m2+1)2)+2/(m2+1))=
=(m2+1)((l-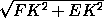/2·
(m+1)/(m2+1))2+(4(m2+1)-(m+1)2)/(2(m2+1)2)).
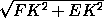/2· (m+1)/(m2+1) .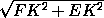
Ответ
при l=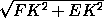/2· (m+1)/(m2+1) .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь