Олимпиадная задача: Площадь "звёздочки" внутри правильного n-угольника с кругами
Задача
Внутри правильного n-угольника со стороной a вписано n равных кругов так, что каждый круг касается двух смежных сторон многоугольника и двух соседних кругов. Найти площадь "звёздочки", ограниченной только дугами вписанных кругов.
Решение
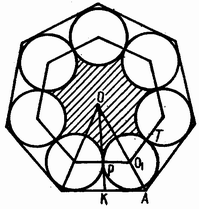
Соединим центры вписанных кругов между собой. Площадь "звездочки" найдём как разность между площадью полученного внутреннего n-угольника (его вершины – центры вписанных кругов) и площадью суммы n секторов вписанных кругов, высекаемых сторонами внутреннего многоугольника (см. рис.).
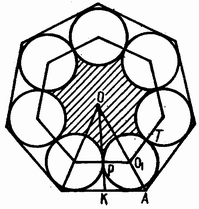
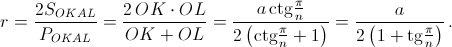Площадь внутреннего многоугольника 
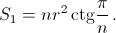Сумма углов всех секторов равна (n– 2)π, поэтому суммаS2их площадей равна сумме площадей n– 2 полукругов радиусаr. Итак, искомая площадь равна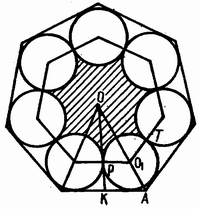 
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет