Олимпиадная задача по многочленам и рациональным функциям для 8–10 классов
Задача
Доказать, что из равенства 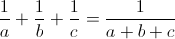 вытекает равенство
вытекает равенство 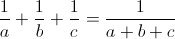 если k нечётно.
если k нечётно.
Решение
Запишем данное равенство в виде (a + b + c)(bc + ac + ab) = abc. Отсюда
0 = (a + b + c)(bc + ac + ab) – abc = (a + b + c)c(a + b) + (a + b)ab = (a + b)(ac + bc + c² + ab) = (a + b)(a + c)(b + c).
Поэтому по крайней мере одна из скобок равна нулю. Пусть, например, a = –b. Тогда при нечётном k ak = – bk, и доказываемое равенство принимает вид очевидного тождества.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет