Олимпиадная задача по планиметрии: точки на BA при MN=3 см, DMN=MNE
Задача
Дан острый угол ABC . На стороне BC отложены отрезки BD= 4 см
и BE= 14 см. Найти на стороне BA такие две точки M и N ,
чтобы MN=3 см и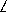 
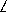DMN= MNE .
Решение
Допустим, что искомые точки M и N найдены, MN – данный
отрезок и 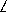DMN=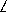 MNE (рис.) Проведём DL||AB и отложим DL=MN (3 см). Соединим точку M с точкой D и N с L . MDLN – параллелограмм. 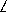BMD=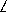 MNL как соответствующие углы
при параллельных MN и DL и секущей AB . 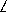BMD=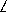 ENA как смежные к равным углам DMA и MNE , следовательно,
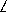MNL=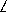 ENA . Опустим из точки L перпендикуляр на прямую AB и
продолжим его до пересечения с прямой EN в точке K .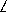
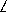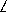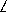KNM= ANE как вертикальные. Поэтому KNM= MNL . KFN= FNL как прямоугольные треугольники с общим
катетом FN и равными острыми углами. Следовательно, KF=FL .
Построив DL||AB и DL=NM , опускаем перпендикуляр из точки L на AB и продолжаем его на отрезок FK=FL . Точку K соединяем с
точкой E и находим точку N в пересечении этой прямой с прямой AB . Откладываем отрезок NM на стороне AB и находим точку M .
Доказательство вытекает из анализа.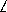
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь