Олимпиадная задача по тригонометрии и логарифмам для 10-11 класса: решить уравнение
Задача
Решить уравнение 2-log sin x cos x=log cos x sin x.
Решение
Для начала выпишем ОДЗ данного уравнения: sin x>0, cos x>0 .
Приведем логарифм в правой части к основанию sin x : 2-log sin x cos x=1/log sin x cos x . После преобразований получим:
(log sin x cos x-1)2=0 или log sin x cos x=1.
cos x= sin x, x=π/4+kπ.
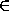
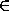 .
.
Ответ
x=π/4+2kπ, k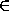
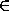 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет