Олимпиадная задача по планиметрии для 8–9 класса: центры вписанных окружностей в прямоугольных треугольниках
Задача
Доказать, что множество центров окружностей, вписанных в
прямоугольные треугольники, гипотенузой которых служит неподвижный
отрезок длиной c , есть дуги окружностей с радиусом c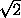 /2 .
/2 .
Решение
Пусть O – центр круга, вписанного в один из прямоугольных
треугольников с гипотенузой c (рис.). Точка O лежит на
биссектрисах углов треугольника. 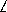 OAC=1/2
OAC=1/2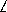 BAC,
BAC,
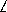 OCA=1/2
OCA=1/2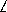 BCA,
BCA, 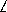 OAC+
OAC+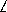 OCA=1/2 (
OCA=1/2 (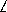 BAC+
BAC+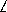 BCA)= 1/2 90o=45o (
BCA)= 1/2 90o=45o ( 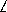 BAC+
BAC+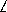 BCA –
сумма острых углов прямоугольного треугольника),
BCA –
сумма острых углов прямоугольного треугольника), 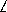 AOC=180o-(
AOC=180o-(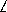 OAC+
OAC+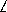 OCA)=180o-45o=135o (из треугольника AOC ). Следовательно, множество центров кругов, вписанных в
прямоугольные треугольники с общей гипотенузой, есть множество
точек, из которых эта гипотенуза видна под углом в 135o . Это –
две дуги, стягивающие хорды, являющиеся сторонами вписанного в круг
квадрата, ибо вписанные в эти дуги углы измеряются половинами дуг в 270o , а значит, сами дуги содержат 90o . Поскольку стягиваемая
этими дугами хорда есть гипотенуза наших прямоугольных
треугольников, то радиус искомых дуг равен c
OCA)=180o-45o=135o (из треугольника AOC ). Следовательно, множество центров кругов, вписанных в
прямоугольные треугольники с общей гипотенузой, есть множество
точек, из которых эта гипотенуза видна под углом в 135o . Это –
две дуги, стягивающие хорды, являющиеся сторонами вписанного в круг
квадрата, ибо вписанные в эти дуги углы измеряются половинами дуг в 270o , а значит, сами дуги содержат 90o . Поскольку стягиваемая
этими дугами хорда есть гипотенуза наших прямоугольных
треугольников, то радиус искомых дуг равен c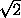 /2 .
/2 .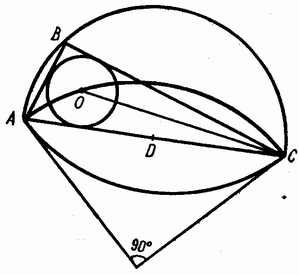
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь