Назад

Олимпиадная задача по планиметрии для 7-9 класса: свойства окружности и четырёхугольника

Задача 208968 • Сложность: 2 • 7-9 класс
Задача

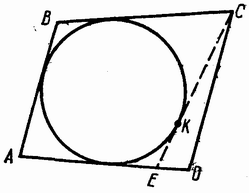
Доказать, что если окружность касается трёх сторон выпуклого четырёхугольника и не пересекает четвёртой, то сумма четвёртой и противоположной ей стороны меньше суммы остальных сторон четырёхугольника.

Разделы:
Планиметрия
Источники:
Белорусские республиканские математические олимпиады Олимпиады и турниры
Количество версий:
5
Решение

Проведем из точки C касательную к окружности (рис.). Получили описанный четырехугольник. Суммы противоположных сторон его равны: BC+AE=AB+CE . Сумма противоположных сторон четырехугольника

BC+AD=BC+AE+ED=(BC+AE)+ED.

Подставим значение BC+AE из первого равенства:

BC+AD=(AB+CE)+ED=AB+(CE+ED).

Из треугольника ECD : CE+ED>CD , поэтому AB+(CE+ED)>AB+CD . Таким образом, BC+AD>AB+CD .

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет