Олимпиадная задача по стереометрии: угол между скрещивающимися медианами в тетраэдре
Задача
Найдите угол между скрещивающимися медианами двух граней правильного тетраэдра.
Решение
 Найдём угол α между мединами DM и AK граней соответственно ADB и ABC правильного тетраэдра ABCD (рис.1). Для этого через центр Q грани ABC проведём прямую, параллельную DM . Пусть эта прямая пересекает
ребро СD в точке S . Тогда искомый угол равен углу между пересекающимися
прямыми QS и AK . Пусть ребро тетраэдра равно a .
Из подобия треугольников QSC и MDC находим, что
Найдём угол α между мединами DM и AK граней соответственно ADB и ABC правильного тетраэдра ABCD (рис.1). Для этого через центр Q грани ABC проведём прямую, параллельную DM . Пусть эта прямая пересекает
ребро СD в точке S . Тогда искомый угол равен углу между пересекающимися
прямыми QS и AK . Пусть ребро тетраэдра равно a .
Из подобия треугольников QSC и MDC находим, что
QS = MD·  =
=  ·
·  =
=  .
.
 CD =
CD = a .
Из треугольника CKS по теореме косинусов находим, что
a .
Из треугольника CKS по теореме косинусов находим, что
SK2 = CK2+CS2-2CK· CS cos 60o =
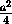 +
+ a2-2·
a2-2· 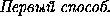 ·
· 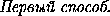 a·
a· 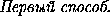 =
=
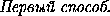 a2.
a2.
cos α = | cos  KQS| = |
KQS| = | | =
|
| =
|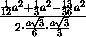 | =
| = .
.
Из подобия треугольников QTR и BER находим, что
QT = BE·  =
= 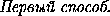 ·
· 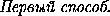 =
= 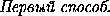 .
.
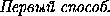 =
= 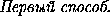 ,
то AT=
,
то AT= 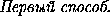 AJ .
Из треугольника ACJ по теореме косинусов находим, что
AJ .
Из треугольника ACJ по теореме косинусов находим, что
AJ2 = AC2+CJ2-2AC· CJ cos 60o =
a2+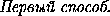 a2-2a·
a2-2a· 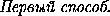 a·
a· 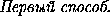 =
=
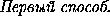 a2.
a2.
 AJ2 =
AJ2 = 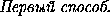 a2.
Тогда из треугольника AQT по теореме косинусов находим, что
a2.
Тогда из треугольника AQT по теореме косинусов находим, что
cos β = | cos  AQT| = |
AQT| = |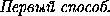 | =
|
| =
|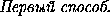 | =
| =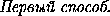 .
.
 Введём прямоугольную систему координат с началом в точке A (рис.3). Ось x направим по лучу AK . Пусть P – проекция точки M на прямую, проходящую через вершину A параллелльно BC . Тогда ось y направим по лучу AP .
Через точку A проведём прямую, параллельную
высоте DQ тетраэдра. Пусть L – проекция точки D на эту прямую.
Тогда ось z направим по лучу AL .
Введём прямоугольную систему координат с началом в точке A (рис.3). Ось x направим по лучу AK . Пусть P – проекция точки M на прямую, проходящую через вершину A параллелльно BC . Тогда ось y направим по лучу AP .
Через точку A проведём прямую, параллельную
высоте DQ тетраэдра. Пусть L – проекция точки D на эту прямую.
Тогда ось z направим по лучу AL .
Тогда интересующие нас точки имеют следующие координаты:
A(0;0;0), K(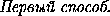 ;0;0),
D(
;0;0),
D( ;0;a
;0;a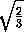 ),
M(
),
M( ;
; ;0),
;0),
B(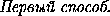 ;
;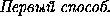 ;0),
E(
;0),
E(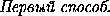 ;0;
;0;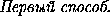 a
a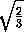 ).
).
 = (
= ( ;0;0),
;0;0),
 =
(
=
( -
- ;
; ;-a
;-a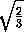 )=
(
)=
(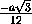 ;
;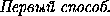 ;-a
;-a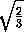 ),
),
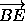 =
(
=
(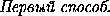 -
-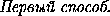 ;-
;-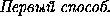 ;
;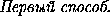 a
a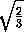 )=
(
)=
(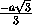 ;-
;- ;
; a
a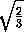 ).
).
cos α = |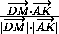 |=
|
|=
|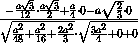 |=
|=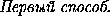 ,
,
cos β = |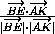 |=
|
|=
|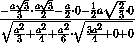 |=
|= .
.
Ответ
arccos  , arccos
, arccos 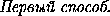 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет