Олимпиадная задача на угол между плоскостями: геометрические методы, 8–9 класс
Задача
Две плоскости заданы уравнениями A1x+B1y+C1z+D1=0и A2x+B2y+C2z+D2=0. Пусть α – величина нетупого угла, образованного плоскостями. Докажите, что
cos α =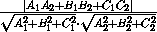
.
Решение
Нетупой угол ϕ между плоскостями либо равен углу между векторами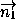 
= (A1;B1;C1)и 
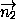= (A2;B2;C2), соответственно
перпендикулярными данным плоскостям, либо дополняет его до90o .
Следовательно,
cos ϕ = | cos α| = |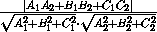
|=
.
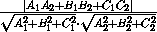Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет