Олимпиадная задача по геометрическим методам для 8-9 класса: уравнение плоскости через точки пересечения с осями
Задача
Плоскость задана уравнением Ax+By+Cz+D=0, причём
числа A , B , C и D отличны от нуля. Докажите,
что тогда уравнение плоскости можно записать в виде 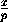 +
+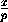 +
+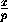 =1, где P(0;0;p), Q(0;q;0)и R(0;0;r)– точки пересечения
плоскости с координатными осями.
=1, где P(0;0;p), Q(0;q;0)и R(0;0;r)– точки пересечения
плоскости с координатными осями.
Решение
Поскольку A 0, B
0, B 0, C
0, C 0и D
0и D 0,
0,
Ax+By+Cz+D=0 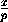 Ax+By+Cz= -D
Ax+By+Cz= -D 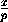 -
-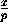 x -
x -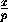 y-
y-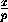 z=1
z=1
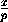
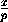
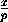 +
+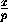 +
+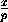 =1
=1
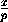
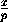 +
+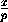 +
+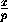 =1,
=1,
p=-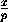 , q=-
, q=-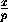 , r= -
, r= -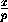 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет