Олимпиадная задача: расстояние от точки до плоскости, геометрия 8-9 класс
Задача
Найдите расстояние от точки M0(x0;y0;z0)до плоскости Ax+By+Cz+D=0.
Решение
Через данную точку M0проведём прямую, перпендикулярную данной
плоскости. В качестве направляющего вектора этой прямой возьмём вектор 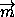 = (A;B;C). Тогда параметрические уравнения прямой
имеют вид
= (A;B;C). Тогда параметрические уравнения прямой
имеют вид
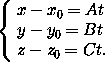
A(x0+ At)+B(y0+Bt)+C(z0+Ct)+D = 0  (A2+B2+C2)t = -(Ax0+By0+Cz0+D)
(A2+B2+C2)t = -(Ax0+By0+Cz0+D) 
 t=-
t=-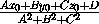 .
.
ρ = M0M = 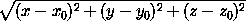 =
=
=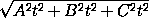 = |t|
= |t|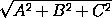 =
=
=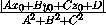 ·
· 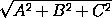 =
=
 .
.
Ответ
ρ =  .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет