Необходимое и достаточное условие принадлежности точки прямой через точку M₀ — олимпиадная задача по геометрии
Задача
Прямая l проходит через точку M0(x0;yo;z0)параллельно
ненулевому вектору 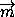 = (a;b;c). Найдите необходимое
и достаточное условие того, что точка M(x;y;z)лежит на прямой l .
= (a;b;c). Найдите необходимое
и достаточное условие того, что точка M(x;y;z)лежит на прямой l .
Решение
Точка M лежит на прямой l тогда и только тогда, когда вектор 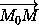 коллинеарен вектору
коллинеарен вектору 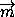 ,
значит,
,
значит,
M(x0;yo;z0) 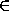 l
l 
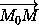 = t
= t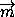


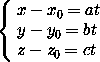

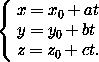
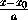 =
=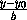 =
=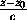 .
.
Ответ
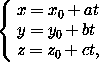 или
или 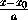 =
=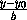 =
=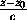 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет