Олимпиадная задача: уравнение плоскости через точку и перпендикулярный вектор
Задача
Составьте уравнение плоскости, проходящей через точку M0(x0;y0;z0)перпендикулярно ненулевому
вектору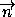 
= (a;b;c).
Решение
Точка M(x;y;z)принадлежит искомой плоскости α тогда и только
тогда, когда вектор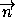 
=(x-x0;y-y0;z-z0)перпендикулярен вектору 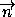. Значит,
M(x;y;z)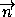 
α 
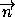
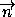
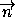
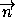
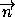
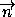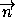· = 0
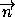
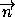a(x-x0) +b(y-y0)+c(z-z0)=0.
Ответ
a(x-x0) +b(y-y0)+c(z-z0)=0.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет