Олимпиадная задача по стереометрии для 8-9 классов: плоскость и пересечение в кубе
Задача
На рёбрах A1B1, AB , A1D1и DD1единичного
куба ABCDA1B1C1D1взяты точки K , L , M и N соответственно, причём A1K = 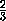 , AL =
, AL = 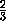 , A1M =
, A1M = 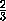 .
Определите, какое из рёбер A1D1или D1C1пересекает
плоскость, параллельную отрезку ML и содержащую отрезок KN . В каком
отношении это ребро делится плоскостью?
.
Определите, какое из рёбер A1D1или D1C1пересекает
плоскость, параллельную отрезку ML и содержащую отрезок KN . В каком
отношении это ребро делится плоскостью?
Решение
Выберем систему координат с началом в точке A1. Ось x направим по лучу A1D1, ось y – по лучу A1B1, ось z – по лучу A1A . Тогда координаты точек K , L , M и N таковы:
K(0;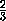 ;0), L(0;
;0), L(0;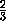 ;1),
M(
;1),
M(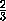 ;0;0), N(1;0;t),
;0;0), N(1;0;t),
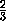 t
t 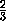 1. Отложим от точки L вектор
1. Отложим от точки L вектор
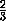 =
=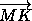 =
(0-
=
(0-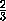 ;
;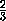 -0;0-0) =
(-
-0;0-0) =
(-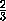 ;
;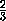 ;0).
;0).
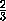 ;
;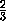 ;1).
Искомая плоскость проходит через точки K , P и N . Ищем уравнение этой
плоскости в виде ax+by+cz = 1. Подставляя в это уравнение координаты
точек K , P и N , находим, что
;1).
Искомая плоскость проходит через точки K , P и N . Ищем уравнение этой
плоскости в виде ax+by+cz = 1. Подставляя в это уравнение координаты
точек K , P и N , находим, что
c=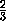 , a=
, a=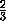 , b=
, b=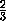 .
.
Подставив нули вместо y и z найдём точку пересечения плоскости с прямой A1D1– x=  , а т.к.0
, а т.к.0 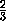 t
t 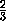 1, то1
1, то1 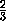 x
x 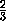
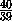 . Значит, секущая плоскость не пересекает
ребро A1D1.
. Значит, секущая плоскость не пересекает
ребро A1D1.
Подставив в полученное уравнение x=1и z=0найдём точку пересечения плоскости с прямой D1C1– y= 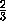 , а т.к.0
, а т.к.0 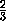 t
t 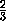 1, то0
1, то0 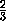 y
y 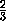
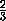 . Значит, секущая плоскость пересекает
ребро D1C1и при этом точка пересечения делит это ребро в любом
отношении от 0 до
. Значит, секущая плоскость пересекает
ребро D1C1и при этом точка пересечения делит это ребро в любом
отношении от 0 до 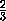 , считая от вершины D1.
, считая от вершины D1.
Ответ
D1C1; в любом отношении от 0 до 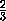 , считая от вершины D1.
, считая от вершины D1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь