Олимпиадная задача по стереометрии: площади проекций треугольника для 8-9 классов
Задача
Площади проекций некоторого треугольника на координатные
плоскости Oxy и Oyz равны соответственно 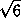 и
и 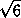 , а площадь проекции на плоскость Oxz –
целое число. Найдите площадь самого треугольника, если
известно, что она также является целым числом.
, а площадь проекции на плоскость Oxz –
целое число. Найдите площадь самого треугольника, если
известно, что она также является целым числом.
Решение
Пусть вектор, перпендикулярный плоскости исходного треугольника, образует с осями координат Ox , Oy и Oz углы α , β и γ соответственно. Тогда
cos2 α + cos2 β + cos2 γ = 1.
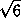 , Sx=
, Sx=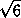 ).
По теореме о площади проекции плоской фигуры на плоскость
).
По теореме о площади проекции плоской фигуры на плоскость
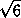 = Sx = S| cos α|, Sy = S| cos β|,
= Sx = S| cos α|, Sy = S| cos β|,
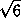 = Sz = S| cos γ|.
= Sz = S| cos γ|.
S2-Sy2 = 13, (S-Sy)(S+Sy) = 13.
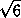
Ответ
7.00
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет