Найдите расстояние между ребрами тетраэдра — олимпиадная задача по стереометрии
Задача
Найдите расстояние между противоположными ребрами правильного тетраэдра с ребром a .
Решение
Решение задачи отсутствует
Ответ
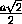 .
.
 Пусть ABCD – правильный тетраэдр с ребром a , M – центр
грани ABC (рис.1). Поскольку DM – высота тетраэдра, угол
между ребром AD и плоскостью грани ABC – это угол DAM .
Обозначим его α . В прямоугольном треугольнике DAM известно,
что AD = a , AM =
Пусть ABCD – правильный тетраэдр с ребром a , M – центр
грани ABC (рис.1). Поскольку DM – высота тетраэдра, угол
между ребром AD и плоскостью грани ABC – это угол DAM .
Обозначим его α . В прямоугольном треугольнике DAM известно,
что AD = a , AM = 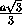 . Следовательно,
. Следовательно,
cos α = cos  DAM =
DAM = 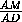 =
=
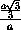 =
= 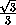 =
=
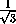 , sin α =
, sin α = 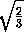 .
.
 BC и DL
BC и DL 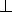 BC , ребро BC перпендикулярно секущей плоскости. Поэтому
высота LF треугольника ADL есть общий перпендикуляр скрещивающихся
прямых AD и BC . Из прямоугольного треугольника AFL находим, что
BC , ребро BC перпендикулярно секущей плоскости. Поэтому
высота LF треугольника ADL есть общий перпендикуляр скрещивающихся
прямых AD и BC . Из прямоугольного треугольника AFL находим, что
FL = AL sin  FAL = AL sin α =
FAL = AL sin α =
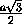 ·
· 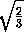 =
= 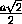 .
.
 Достроим правильный тетраэдр ABCD до параллелепипеда, проведя
через его противоположные ребра три пары параллельных плоскостей (рис.2).
Поскольку противоположные ребра правильного тетраэдра попарно равны
и перпендикулярны, построенный параллелепипед – куб, диагональ
грани которого равна a . Расстояние между противоположными ребрами
тетраэдра равно ребру этого куба, т.е.
Достроим правильный тетраэдр ABCD до параллелепипеда, проведя
через его противоположные ребра три пары параллельных плоскостей (рис.2).
Поскольку противоположные ребра правильного тетраэдра попарно равны
и перпендикулярны, построенный параллелепипед – куб, диагональ
грани которого равна a . Расстояние между противоположными ребрами
тетраэдра равно ребру этого куба, т.е. 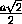 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет