Олимпиадная задача по планиметрии и комбинаторной геометрии для классов 6-9 про треугольники
Задача
Есть три треугольника: остроугольный, прямоугольный и тупоугольный. Саша взял себе один треугольник, а Боря – два оставшихся. Оказалось, что Боря может приложить (без наложения) один из своих треугольников к другому, и получить треугольник, равный Сашиному. Какой из этих треугольников взял Саша?
Решение
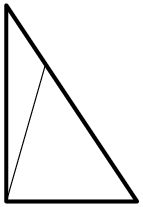
Саша может разрезать одной прямой свой треугольник на два, равных Бориным. При этом один из концов разреза расположен в вершине Сашиного треугольника, а другой – на противоположной стороне.
Посмотрим на сторону, которую пересёк разрез. Разрез не перпендикулярен этой стороне (иначе получится два прямоугольных треугольника, что противоречит условию). Значит, получится один тупоугольный треугольник и один остроугольный или прямоугольный.
В первом случае Сашин треугольник – прямоугольный. Пример приведён на рисунке.
Ответ
Прямоугольный.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь